Workshop: Treasury Systems – het waarom en hoe (niet) van Treasury & Banking Software

| 02-06-2016 | treasuryXL


workshop Financial SystemsOp 26-05-2016 waren treasuryXL en Treasurer Search aanwezig op Financial Systems. Naast dat we een stand op de beursvloer hadden, hebben we ook een invitation only sessie georganiseerd: Treasury Systems – het waarom en hoe (niet) van Treasury & Banking Software. Hiervoor hebben we vier interim managers uitgenodigd die elk hun eigen gekozen topics kwamen pitchen. De deelnemers van de workshop waren vrij om vragen te stellen en aan te vullen waar nodig. Het resultaat was een geslaagde en interactieve sessie waaruit we ook voor treasuryXL inspiratie konden putten.

Op voorhand hebben we een aantal doelen gesteld voor deze sessie:

  • Ontwikkelingen op het snijvlak Treasury & Financial Systems doornemen
  • Voor leken: overview & duiding
  • Voor experts: verdere verdieping en bruggen slaan
  • Voor treasuryXL: inventarisatie informatiebehoefte
  • Voor allen: bepalen met wie je mogelijk volgende stappen wilt zetten

De vier interim managers aan het woord

Hieronder volgt een korte samenvatting van de presentaties van de vier interim managers met (indien aanwezig) reacties uit de zaal.

Erik Teiken

Erik TeikenAccounting in je TMS – zijn er voordelen?
Een TMS heeft vaak accounting modules maar deze worden niet altijd vanaf het begin meegenomen voornamelijk vanwege de kosten en extra tijd en inspanning voor de inrichting ervan. Toch zijn er wel voordelen voor het meenemen van een accounting module in je TMS en na verloop van tijd wordt er vaak toch tot aanschaf overgegaan. Dit heeft volgens Erik te maken met drie punten:

  • Na intensiever gebruik blijkt de accounting module toch nodig door de hoeveelheid deals, wat lastig aan te sluiten is met ERP.
  • Ook de complexiteit van bijvoorbeeld exotische deals heeft vaak invloed. Door een accounting module kun je alle verplichtingen in je TMS ook meenemen.
  • Ook Hedge Accounting volgens IFRS heeft zo zijn voordelen bij het implementeren van een accounting module, het wordt makkelijker te automatiseren. De treasurer wil inzicht in eigen p&l verantwoording, EMIR.

Marktsystemen – toeters en bellen?
Er zitten natuurlijk voordelen aan het aanschaffen van een systeem als Reuters of Bloomberg. Het levert de treasurer actuele marktinformatie op; informatie over valuta´s, interest en nieuws. Op langere termijn kun je zien hoe de yield curve loopt en levert het toegevoegde waarde op; je kunt scenario’s ontwikkelen over exposure in de toekomst en daar kun je je strategie op aanpassen. Er zijn toeters en bellen die waarschuwen. Een nadeel van het aanschaffen van een marktsysteem is het kostenplaatje: zo’n 15-20K per jaar.

Static Data in je TMS – levert het wat op?
Static data lijkt het ondergeschoven kindje te zijn in een TMS, en wordt als droog en saai ervaren. Het gevaar van je static data niet op orde hebben is dat je veel tijd verliest met zoeken van essentiële data. Geen match met ERP is nog wel te overkomen maar wat als betalingen op verkeerde rekeningen terecht komen of niet uitgevoerd kunnen worden?
Het is dus van belang dit op orde te hebben maar ook om functiescheiding toe te passen; iemand voert in en iemand controleert de invoer. In treasury kan elke fout kostbaar zijn voor een bedrijf.

Menno van Suylichem

Menno van SuylichemWelke variabelen bepalen je systeemkeuze?

De doelen van een implementatie zijn kostenreductie, efficiency en risicobeperking. Variabelen die de systeemkeuze bepalen zijn onder meer: cloud versus stand-alone applicatie, functionaliteiten, modulaire opbouw, integratie met bestaande ERP systemen, reporting tools, ondersteuning leverancier, toegankelijkheid en kosten.

Voordat je überhaupt kan overgaan tot implementatie dienen de bestaande static (basis) data goed bereikbaar te zijn en gecontroleerd te worden, eventueel aangevuld met nieuwe informatie. Houdt hierbij zoveel mogelijk rekening met nieuwe (toekomstige) functionaliteiten/gebruik van het systeem.

Wat wil ik als bedrijf, wat heb ik echt nodig aan informatie, nu en in de nabije toekomst. Niet alle applicaties van een systeem zijn (direct) van toepassing. Start met de meest noodzakelijke, d.w.z. de applicaties die de dagelijkse processen en de daaruit voortvloeiende beslissingen/risico’s direct ondersteunen en beperken.

Implementatie outsourcen of zelfstandig?
Bedrijven onderschatten vaak hoeveel tijd het kost om een TMS zelf te implementeren. Reken op 12 tot 18 maanden, waarbij een persoon binnen de organisatie moet worden vrijgemaakt. Deze kennis verdwijnt vervolgens als diegene van functie veranderd of het bedrijf verlaat
Uit de zaal komt de input dat je bij het zelf implementeren alles zelf in de hand hebt, bij outsourcing zit de leverancier er niet zo midden in en weet dus niet exact wat er wel en niet nodig is. Reactie hierop is dat een goede blueprint van belang is en dat je de leverancier duidelijk opdracht kan geven over wat jij wel of niet wilt.

Inrichting systeem moet binnen de bestaande procuratieschema’s passen

Het is belangrijk de toegang tot een TMS goed in te richten. Houd ook in de gaten hoe het voorheen zat; wie mag transacties invoeren, wie mag transacties afsluiten, wie mag deze transacties invoeren en wie mag de hieruit voortvloeiende betalingsopdrachten tekenen? Meerdere mensen geven aan vaker tegen procuratie aan te lopen. Vooral omdat ze in de praktijk nog nooit hebben meegemaakt dat het hiermee mis ging.
Procedurele controle is belangrijk, dit wordt ook door de deelnemers in de zaal bevestigd, altijd alles met gescheiden autorisatie; één persoon voert in en één persoon geeft akkoord. 

Dick Bennink

Dick BenninkSysteem dwingt altijd tot aanpassingen in huidige proces – wees voorzichtig met customizen
Doe aan pakketselectie. De leverancier zegt misschien dat het kan maar tijdens de daadwerkelijke implementatie blijkt toch dat het net niet kan of helemaal niet kan. De mensen die werken bij de leveranciers zijn niet altijd werkzaam in treasury, en sluiten niet altijd goed aan op de praktijk. Systemen zijn niet perfect, probeer een balans te vinden in het veranderen of de kleine aanpassing. Blijf uit de buurt van hele grote veranderingen. Dit brengt hoge kosten met zich mee en maatwerk leidt tot een hoop extra werk.

“Meenemen” en “meekrijgen” van alle (internationale) ondernemingen bij een implementatie
Implementeren blijkt vaak een ‘hoofdkantoor-feestje’ te zijn, je bent afhankelijk van dochterondernemingen. Hoofdzaak is om mensen lager in de organisatie te laten helpen om de implementatie tot een succes te maken. Luister naar de dochterondernemingen om te zorgen dat de workload die jij aan ze oplegt om het systeem te voeden, te doen is. Kijk of er dingen in het systeem zijn die je terug kunt geven, bijvoorbeeld om de werkzaamheden makkelijker of efficiënter te laten verlopen. Zorg voor een duidelijke blueprint om aanpassingen in het lopende proces te minimaliseren. Onafhankelijk van wat je doet, zorg dat je binnen 3 maanden succes kunt vieren.

Olivier Werlingshoff

Olivier WerlingshoffSystemen maar Cash Awareness is de basis!
Cash awareness is belangrijk, er wordt veel gehamerd op TMS, rapportages en analyses. De basis is dat datgene dat ingevoerd wordt voor de liquiditeitsplanning ook zorgt voor een goede planning.

Bij liquiditeitsplanningen is de business leidend en niet de systemen
Collega’s uit de organisatie weten vaak veel beter wanneer bepaalde stromen werkelijk binnen zullen komen en eruit zullen gaan. Hetgeen dat de business aangeeft is bepalend voor de planning.

Toegang tot de TMS voor de Business
Het kan handig zijn om bij input vanuit de business de persoon verantwoordelijk te maken voor hetgeen waar ze input voor hebben gegeven, zo creëer je cash awareness binnen de organisatie omdat mensen zich betrokken voelen, verantwoordelijkheid voelen voor hetgeen ze hebben aangegeven en veranderingen worden sneller doorgegeven. Tot slot is het hiervoor handig om toegang tot de TMS te geven aan collega’s uit de business om de input te kunnen doorgeven en/of de planning te kunnen controleren.

De sessie samengevat

Het was een geslaagde, interactieve workshop die nieuwe inzichten met zich meebracht. Samen met de aanwezigen waren we het er over eens dat er een aantal onderwerpen zijn waarbij nog meer verdieping nodig is:

  1. Static data
  2. Integratie tussen systemen
  3. Blueprint
  4. Procuratie
  5. Cash awareness, (vergeten kindje, koppelen met business)
  6. Surrealistische gesprekken met leveranciers.
  7. Binnenhengelen onderliggende partij, geven en nemen

Over deze onderwerpen zullen in de komende tijd dan ook artikelen verschijnen op treasuryXL. Heb je interesse om een artikel te schrijven over een van deze onderwerpen? Neem dan contact met mij op via [email protected].

Ook namens Treasurer Search willen we alle aanwezigen bedanken voor hun komst en input. We hopen in de toekomst meer van deze interessante sessies te kunnen organiseren.

Stephanie DerkseStephanie Derkse
Community Manager

[email protected]
06-21303744

Innovation in Treasury Management: Vallstein’s walletsizing

31-05-2016 | Huub Wevers from Vallstein

On april 13th of this year the Fintech innovation awards took place. Vallstein won the innovation award in treasury management with their Walletsizing® system. We asked Huub Wevers from Vallstein to give us an update on this new system. What’s new about it and who will benefit from using Walletsizing®?

Congratulations on winning the award, can you tell us more about WalletSizing?

WalletSizing® is a system in the cloud focused on giving full transparency to corporates on their spending and profitability for banks. All their banks globally, regardless of the number of banks and the type of products, varying from Fx, Cash Management, bonds, lending or asset management. We take in all data a corporate has available on the products and invoices from the bank in an innovative easy way for the corporate where they do not need to do much with the data. We translate, map and upload it into the system after which the corporate has all insight in their banking landscape and can do easy analysis with all the features the system offers.

What distinguishes WalletSizing® from its competitors?

Firstly, WalletSizing® looks at the entire bank relationship, across all product areas, not just transaction services or credit, but everything that is being used from all banks that maintain a relationship with the client concerned. Secondly, we take an explicit view through the eyes of the bank on the relationship, taking all relevant Basel III /IV regulation into account. This kind of transparency is absolutely essential to identify the real room to negotiate and ensure terms and conditions that are truly fair for both sides of the table. Thirdly: technology. We provide analysis for clients maintaining multiple bank relationships across a multitude of countries with many different banking products, which is impossible to build and let alone maintain in spreadsheets.

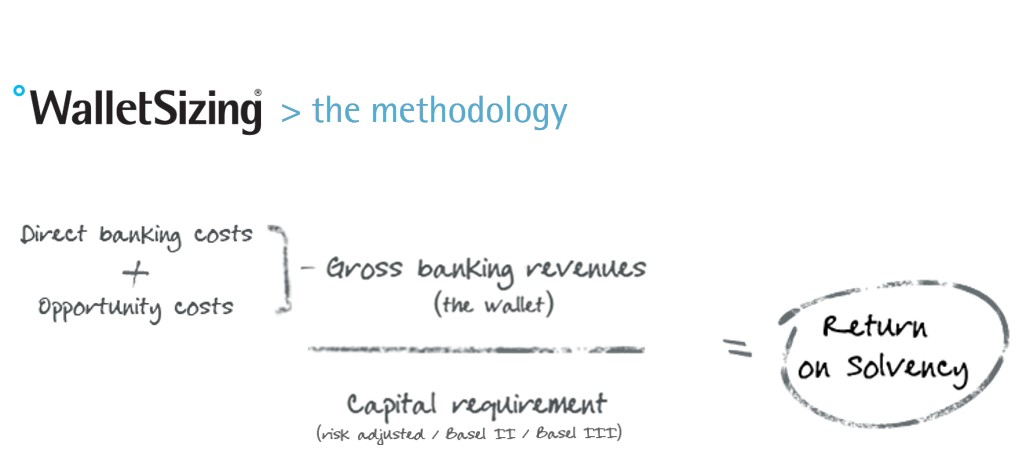
ROS Calculation 2

 

Who will benefit from using this system?

CFO’s and Treasurers will benefit by having full transparency in the bank relationships and as a result they will have more meaningful bank reviews, RFP’s and Negotiations. Depending on the objectives a corporate has, it will allow them to be fair in their distribution of business towards banks, limit the number of banks used globally or keep banks costs in line with market practice as will be indicated by the system’s benchmarking capabilities. Where cost saving was an objective, corporates saved 26% on their bank costs on average, across the entire relationship, all products.

Vallstein won the Fintech innovation Award 2016, what is innovative about your system?

We take away the need for extensive data gathering, translating and analysis by taking this responsibility upon us and we create full transparency using all data and the latest Basel III rules in a matter of days. Comparing banks like for like. Next to this we have extended the functionalities last year by having a edition focused on Bank Fee Analysis as well. The system verifies automatically after upload of new invoices if the prices paid are as agreed earlier with the banks. A simple and somewhat more operational step.

Can you give some examples of companies and employees that are using Walletsizing®?

Examples of Companies that are currently using WalletSizing® are SaudiAramco, Salzgitter, Vimpelcom and many more. Typically, the Treasury Control department works with the system on a day to day basis and depending who is having the bank reviews the Treasurer or CFO will be using the reporting.

 

Picture_HWHuub Wevers is responsible for Corporate Solutions at Vallstein, the leading Bank Relationship Management specialist. Before joining Vallstein he has had eighteen years of experience in Banking at ABN AMRO and RBS, notably Transaction Banking. His responsibilities included Product Management, Account Management, Implementation and Operations, whereby his last role was the leadership of all Service & Operations in EMEA for RBS. At Vallstein Huub is responsible for building out the software solutions that Vallstein offers for corporates. Solutions that automate bank relationship management in order to assess the profitability that a corporate has for their banks, using all banking products and Basel III.

Option Tales: Cheap Options Part III

| 31-05-2016 | Rob Söentken

banking

 

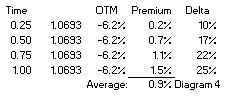
Today in Rob Söentken’s Option Tales: When buying options it is tempting to see if the premium expenses can be minimized. A number of solutions are possible, which will be discussed in four articles. In the previous article I talked about choosing the longer tenor and the compound option. Today I will discuss the average rate option (ARO) and the conditional premium option.

Average Rate Option (ARO)

An Average Rate Option (ARO) can be misleading because it is like a vanilla option except for the reference rate against which it is exercised. The reference rate for an ARO is an average based on spot rates for USD taken at predetermined intervals. For a vanilla option it is the single rate for spot at maturity. If the intention was to hedge the rate for USD in 1-year time, the average of USD rates during the year is really something different.

If we would be looking to hedge a 1-year tenor and the averaging would be at quarterly intervals, a rough and quick estimate of an ARO’s cost would be the average premium of separate vanilla options for respective tenors, in this case that would be 0.9% (see diagram 3). Which would be considerably less than a vanilla option costing 1.50%.average rate option ARO
But unlike a strip of options which can be exercised individually, an ARO can only be exercised in total. At maturity the averaging of the fixings is mostly done, and it could happen that while the last fixing is In The Money (ITM), the average of the fixings is not, making the ARO expire worthless. In this example it would be advantageous to have a strip of vanilla options because each option would be exercisable independently of the other. The ARO on the other hand is worthless because the average would still be above the strike. This inherent risk in using an ARO will make the premium of an ARO even a bit cheaper than a strip of vanilla options.

The bottom line remains that the premium of an ARO is lower than a vanilla option for the same tenor, because the embedded tenor of the ARO is really shorter. The effect is comparable to paragraph 2 ‘Choose shorter tenor’. Slightly worse even when considering the averaging effect.

Conditional Premium Option

A Conditional Premium Option has the advantage over a vanilla option in that premium only has to be paid if the option is In-The-Money (ITM). But… if the option is ITM the premium will be a multiple of a vanilla option. The premium of such a Conditional Premium Option is calculated by dividing the premium of a vanilla optionconditional premium option (1.5%, see diagram 5) by the chance it will be exercised (Delta, in this case 25%), ie 1.5% : 25% = 6%. It could be a very disappointing to find that if this Conditional Premium option is only marginally ITM at maturity, because the premium of 6% still has to be paid.

A Conditional Premium Option is constructed by buying a vanilla option and selling a digital option with the same strike. The digital option will be for a payout of 6% and because it also has a chance on exercise of 25% it will generate 1.5% premium, offsetting the premium of the vanilla option.

Next week in the last Option Tales article; the Reverse Knock-Out Option (RKO).

Would you like to read more on Rob Söentken’s Option Tales?:

1. Options are for wimps

2. ATM or OTM

3. Cheap Options part I

4. Cheap Options part II

 

Rob Soentken

 

 

Rob Söentken

Ex-derivates trader

In de praktijk: Derivaten in de zorgsector

| 30-05-2016 | Willem van Overveld |

Willem van Overveld beschrijft hoe een simpele SWAP constructie zonder margin calls toch lastig kan worden: de menselijk organisatorische kant van derivaten constructies krijgt vaak te weinig aandacht. Een voorbeeld uit de praktijk:

 

Het jaar 2012-2013: In een niet nader te noemen financieel zeer rendabel en solvabel ziekenhuis in midden Nederland was een bouwproject gaande ter grootte van 280 mln. euro. Het was vanwege marktomstandigheden niet mogelijk geweest om het financieringsvolume met gangbare leningen aan te trekken. De externe treasury adviseur had aangegeven dit tekort op te kunnen lossen met een renteswap. Onder toeziend oog van toezichthouders werd een renteswap aangekocht, die stapsgewijs opbouwde tot deze 280 mln., en in twintig jaar tijd weer afloste.

De renteswap wisselde 3 maands Euribor voor 3,5% lang met een risico-opslag. Tranches kasgeld onder de renteswap werden aangetrokken met de bouwfacturen die wekelijks binnenstroomden volgens een vaststaand schema. Voordat er een bouwfactuur werd goedgekeurd, werd er een rondleiding op de bouwlocatie gehouden met een bouwkundig opzichter die ook affiniteit had met bancaire diensten. Een extra bankmedewerker was ingehuurd om de verlenging van de kasgelden voor ons uit handen te nemen.

Zo op het eerste gezicht leek de derivatenconstructie een win-win situatie voor alle partijen. Het ziekenhuis kon bouwen en betaalde een vaste nette rente, de bank kon financieren, verdiende op het hoogtepunt 2,8 mln. per jaar (1% winstopslag op een volume van 280 mln.) en de groeiende Vinex wijk was verzekerd van passende zorg. De ratio’s van het ziekenhuis liepen netjes en voorspelbaar binnen alle grenswaarden die met de banken en WSF waren afgesproken.

Voordat ik aantrad als vaste treasury officer was de situatie aan het kantelen. De bedenker van de constructie en de HEAD waren van baan gewisseld en het ziekenhuis had er geen rekening mee gehouden dat er schaarse kennis nodig is om een dergelijke constructie goed te kunnen administreren. De enige persoon die die kennis had was de HEAD zelf, gesteund door externe adviseurs. Zo was men in het ziekenhuis wel op de hoogte dat de IRS (de swap van Rob heette die inmiddels) steeds hogere rentebetalingen vergde, maar men wist niet dat er ook daadwerkelijk geld opgenomen moest worden. (Er is voldoende liquiditeit op de bank en lenen doe je zo min mogelijk toch?) Het gevolg was een SWAP met een verschil tussen werkelijk opgenomen kasgeld van zo’n 60-70 mln. euro.

Een inefficiënte SWAP, waarbij je rente betaalt voor bedrag ‘x’ en kasgeld hebt opgenomen voor bedrag ‘y’ is prettig voor een bank, en hoeft ook nog geen echt probleem te zijn voor een ziekenhuis als de rente niet te hoog of te laag is. Bij mijn aantreden was de Euribor al hard op weg om naar 0 te gaan. Het gevolg was dat de marktwaarde van de SWAP zeer negatief was. We wisselden 3,5% rente voor 0% Euribor: een dure verzekering. Mede ook omdat de effectieve rente over het opgenomen bedrag tussen de 6 en 7 procent lag ontstond er een situatie die aan de toezichthouders niet meer uit te leggen was.

Ik kreeg de instructie om dit probleem op te lossen. Tijdens mijn proeftijd begon ik al de noodzakelijke beleidsrapporten te schrijven, bouwfacturen te verzamelen en liquiditeiten ter grootte van 40 mln. op te nemen. Doel daarvan was om niet in de jaarrekening te hoeven vermelden dat de marktwaarde van de swap 60 mln. negatief was. De accountant kreeg de opdracht een RFP uit te schrijven. Kostprijs hedge accounting kun je alleen toepassen bij een swap die redelijk nominaal loopt. Omdat facturen voorspelbaar waren, was dat gedeelte in een paar weken door mij opgelost. Echter er was ook een vrij te besteden tranche van 23,5 mln. voor vaste medische apparatuur in het nieuwe ziekenhuis maar er was geen investeringsbegroting naar de inkoopafdeling gegaan. Inkopers zijn opgegroeid met Hollandse zuinigheid. Zij moesten tegen hun vakprincipes in zoveel mogelijk geld uitgeven voor medische apparatuur die zij wellicht in goede staat elders in het ziekenhuis konden vinden.

Op het hoogtepunt van mijn interventie stond er 60 mln. aan liquiditeiten op de bankrekening. Om ons heen vielen allerlei bedrijven om door liquiditeitsproblemen. Bij ons liep het geld langs de muren naar beneden. Even hebben we getwijfeld of we zelf geen bank moesten spelen. Dat leverde meer op dan de 0,2% rente die we zelf ontvingen op onze rekening courant. Ik kreeg geen mandaat om gedeelten van het geld elders onder te brengen: te lastig, risicovol, niet conform treasury statuut etc.

Ook in de rentenacalculatie waren er dingen mis gegaan. Ik ontdekte dat er 1,5 mln. euro te weinig was nagecalculeerd aan de broodheren van het ziekenhuis: de zorgverzekeraars. Ook hier had de Hollandse zuinigheid een rol gespeeld: bruto swapbedragen betalen en netto bedragen nacalculeren. NZA (Nederlandse Zorg Autoriteit) oordeelde dat er een lek in de wetgeving was ontstaan en ze geen middelen hadden om een ziekenhuis te ontzeggen de bruto SWAP bedragen in rekening te brengen. Wij zetten door en kregen ons gelijk. We hadden snel 1,5 mln. verdiend. Na deze reparatie actie werd mij een andere baan aangeboden.

Ik hoorde dat de NZA was ingevallen in de week nadat ik van baan was gewisseld. Dit had niets met treasury te maken, maar met verkeerd gedeclareerde zorgproducten. Het ziekenhuis kreeg 20 mln. euro boete opgelegd. Gelukkig had het betreffende ziekenhuis genoeg liquiditeit op de bank staan op dat moment.

De veelbelovende, maar wat stagnerende Vinex wijk waarin gebouwd werd, is later qua bouwvolume woningen ook bijgetrokken.

Willem van Overveld – Allround finance / treasury professional
[social_links size=”normal” align=””  linkedin=”https://www.linkedin.com/in/willemvanoverveld”]

 

Yield Curves (term structure of interest rates) – filling in the blanks

| 27-05-2016 | Lionel Pavey

Most treasurers do not have access to a dedicated financial data vendor (Bloomberg, Reuters) but are regularly faced with having to discover prices related to yield curves. There are websites that can provide us with relevant data, but these are normally a snapshot and not comprehensive – the data series is incomplete. It is therefore up to the treasurer to complete the series by filling in the blanks.

A quick refresher about the construction of a yield curve raises the following points:-

  • All data must be from the same market (treasury bonds, Interest Rate Swaps (IRS) etc.)
  • A regular term (maturity) is preferred for ease of construction
  • A curve must be smooth
  • An implied zero yield curve can be built from the smooth par curve – a theoretical yield curve where no interest is paid until maturity. In a bond this would redeem at par (100) and be issued at a deep discount to par
  • A series of discounted cash flow factors (DCF) are produced
  • An implied forward curve with constant maturities can be built from the par curve
  • An implied forward curve must be monotonic – each point in an increasing sequence is greater than or equal to the preceding point, each point in a decreasing sequence is smaller than or equal to the preceding point

If we look at IRS par yield prices that can be found on a website, we can regularly see yield prices for periods from 1 year to 10 year inclusive, a 15 year price and a 20 year price. To construct a complete curve from 1 year up to and including 20 years we need to fill in the blanks at 11,12,13,14,16,17,18 and 19 years. These yields are assumed to be par yields – the coupon rate is equal to the yield to maturity and the instrument trades at par.

Before starting let us define the procedure for constructing a par yield curve:-
The methodology used is called “bootstrapping”. This allows us to extract discount factors (DCF) from the market rates. DCF’s allow us to calculate a value today for a cash flow in the future.

We assume that the nominal value for all calculation purposes is 100

For a 1 year rate we know the interest and redemption amount at maturity. A DCF is built whereby the net present value (NPV) of these future cash flows in 1 years’ time is equal to 100 or par.

For a 2 year rate we receive interest after 1 year and interest and redemption amount at maturity.

We discount the 1st years’ interest with the DCF we obtained from the 1 year rate and deduct this amount from our initial nominal of 100. This net amount is then divided by the interest and redemption at maturity (at end of 2 years) to obtain the DCF for the 2 year rate.

Example:

1 Year                                      7%                          2 Year                          9%

1 Year      
100 / (7/100+100) = 0.93457944 (DCF)

2 Year
9 * 0.93457944 = 8.41121496
100 – 8.41121496 = 91.58878504
91.58878504 / (9/100+100) = 0.8402640829

These DCF’s can then be used to find the NPV of any cash flow maturing in 1 or 2 years’ time.

The following example shows a yield curve from February 2013 published on the website of an interbank broker.

yield curve February 2013

yield curve February 2013

The quickest way to price the missing periods would be with straight line interpolation of the par curve between the known points – which would produce the following par curve, zero yield curve and forward curve with constant 1 year maturity.

yield curve February 2013 - 2

yield curve February 2013

Straight line interpolation

Straight line interpolation

 

Whilst the par curve and zero curve are smooth, the implied 1 year constant maturity curve is jagged and certainly neither smooth nor monotonic. The 11th 1 year period rate is lower than the 10th period and the 15th 1 year period rate is higher than the 16th period.

A second approach would be to apply a weighting to the known periods of the par curve and to average the difference out over the missing periods. Read more on this second approach in my next article which will appear next week.

Lionel Pavey

 

 

Lionel Pavey

Treasurer

 

 

Coco goes Loco!

26-05-2016 | by Pieter Jan van Krevel |

The title of this article does not pertain to mademoiselle Coco Chanel losing her marbles, nor to a small, furry animal going berserk over its squeaky toy. In this case, it refers to the Contingent Convertible bond (‘Coco’): a financial instrument that lately seems to have fallen from grace with the investment crowd.

While contingent convertibles exist on other securities for some time now, since the last financial crisis they have become quite popular amongst banks that use them to prop up their core tier 1 capital[1]. Similar to the hybrids from an almost bygone era, Cocos are hybrid securities that allow banks to consider them as equity. Why? Because they will either convert into equity, or be written off, if tier 1 capital falls below a preset threshold.[2] Cocos are (thus) heavily subordinated and carry a commensurate yield.[3] Or at least so it appeared.

Why then is their reputation going south? A first hiccup in their rise to popularity was caused by the implementation of the Basel III regime, under which not all Cocos are eligible for inclusion in tier 1 capital. Cocos with clauses on regulatory changes allow early redemption in that event, and when Lloyds wanted to call USD 5bn worth of Cocos on this ground, (legal) hell broke loose. Recently the UK Court of Appeal announced it would consider the previous appellate ruling allowing early redemption. The jury is still out, so to say.

This is not the only clause that can spoil the investors’ party. Common others are the issuer’s right to (indefinitely) skip interest payments, or postpone redemption. The latter can be as simple as just not call a callable perpetual, and thus ‘convert’ a Coco previously priced to first call in, say, 5 years, into an ‘real’ perpetual. Imagine what that does for NPV…!

Coco’s popularity took another hit last February, when rising concerns about Deutsche Bank’s performance – and even viability – triggered speculation about DB having to skip coupon payments on its Cocos, caused by some rather obscure accounting idiosyncrasy. Chaos quickly spread to other Cocos, bank stocks and bonds alike.

UBS‘ March 14 issuance of a new USD 1.5bn Coco proves things have quieted down somewhat, but investors have become more aware of both the complexity and the risks Cocos bear. It seems that the market is realizing that, as ever, there is no such thing as a free lunch. Not even a meagre loaf of coco bread.

[1] First Coco issued in November 2009 by Lloyds Banking Group, with Rabobank following suit in March 2010.

[2] Some, qualifying, Cocos are also referred to as ‘AT1’ – Additional Tier 1. These are considered the riskiest debt issued by banks.

[3] The 2010 Rabobank issue was e.g. priced at 300bps over a similar but non-convertible loan.

Pieter Jan van Krevel

 

Pieter Jan van Krevel

Owner at Slàinte Mhath!

Treasury Education: great but do not expect career miracles. Do make a strategy.

| 25-05-2016 | Pieter de Kiewit |

studyLast week I visited an information session about financial postgraduate education. It was organized by the VU (Vrije Universiteit, Amsterdam). I noticed an increased interest in comparison to last years session, which is great. Information was provided about courses I see back in the CV’s of treasurers: CFA, RBA (Register Belegging Analyst) and of course RT (Register Treasurer) that has an overlap with the ACT courses. Education, specifically postgraduate, is a topic that returns in many of my meetings. This is what I notice on the topic:

Investing in education is like investing in your network: if you start thinking about it when the need is urgent, you are too late and you will have to work harder. Education as a topic comes up, most of the time, when somebody is planning his career strategy, being in a position or when somebody is between jobs. In the first situation I often notice an intrinsic motivation, eagerness for knowledge and curiosity about other people’s experience. Elements for a solid basis to complete the education.

Candidates that lack these elements often have a harder time to complete their education. Even when they are willing to invest their own money. Furthermore, candidates that are between jobs are open for a broader range of positions than those who search from being employed. This makes it harder for the unemployed to choose which education to pursue. To complete this negative list, regretfully employers often do not have a good understanding of the value of specific treasury courses. In our assignments postgraduate treasury education is hardly ever a dealmaker or a deal breaker.

This is not a plea to stop learning! Treasury education is always great. Sometimes timing can be improved. This is a plea to plan ahead, about your career and education.

If you want to brainstorm, contact me. And let me know what your thoughts are.

Pieter de Kiewit

 

 

 

Pieter de Kiewit
Owner Treasurer Search

 

 

Option Tales: Cheap Options Part II

| 24-05-2016 | Rob Söentken |

bankingToday in Rob Söentken’s Option Tales: When buying options it is tempting to see if the premium expenses can be minimized. A number of solutions are possible, which will be discussed in four articles. In the previous article I talked about the first two solutions: Choose the strike further OTM and Choose shorter tenor. Today I will be discussing the next two solutions: Choose the longer tenor and the Compound option.

 

3- Choose longer tenor

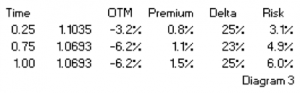Following the comparison between a 3-month and a 12-month option, it should be remembered that a 12-month option will have some remaining value after 3 months have passed, at least theoretically. If we assume ‘ceteris paribus’ (everything remained unchanged) the remaining option value of a 12-month option would be 1.1%. If we diagram1pt2bought the option for 1.5%, we could sell it after 3 months at 1.1% and buy the USD through an outright forward transaction. This approach shows that the net cost of option protection would be only 0.4% (1.5% – 1.1%). Which would be cheaper than the premium of a 3-month option with the same Delta. Also, because the option has a higher Delta than a 3-month option with the same strike (25% vs 10%, see diagram 2), it will follow the spot market much better. The bottom line of paragraph 3 is that a longer dated option can be bought with the intention to sell it again at some point, the net cost being less than buying a shorter dated option. While it serves as a hedge against price changes.

4- Compound option

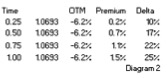A compound option is the right to buy an option against a certain premium. For example we could be considering todiagrampt2 buy the 1-year option in diagram 2 for 1.5%. Alternatively we could consider buying a right to buy this option for 0.4% in 3 months time. At that time the 1-year option will only have 9 months remaining, but the strike and 1.5% premium are fixed in the contract. On the expiry date of the compound option we can decide if we want to pay 1.5% for the underlying option. Alternatively, assuming nothing has changed, we could buy a 9 month option in the market for 1.1% (see diagram 2). In such a case we wouldn’t exercise the compound option.

An alternative to the compound option would be to buy the 3-month option for 0.2%. On expiry, assuming nothing has changed again, we could buy a 9 month option in the market for 1.1% (see diagram 2).

In my next two articles I will discuss the last two solutions for minimizing premium expenses when buying options:

  • Conditional Premium option
  • Reverse Knock Out

Would you like to read more in Rob Söentken’s Option Tales?
1. Options are for wimps
2. ATM or OTM
3. Cheap options part 1

 

Rob Soentken

 

 

Rob Söentken

Ex-derivatives trader

 

Cash flow forecasting (CFFC)

23-05-2016 | by Udo Rademakers |

In recent years and months, we have seen quite a few companies coming into liquidity problems, leading in worst case scenario to insolvencies. This brings us to the question: how important is cash flow forecasting? How to anticipate adequately and to avoid facing “surprises” at the last moment and how should you implement it?
The Cash flow forecast (CFFC) estimates the timing and amounts of cash in- and outflows over a specific period and in different time buckets (day, week, month, year). It provides you with an actual overview of the cash position and with a forecast.

Why is a cash flow forecast important?

  • based on the CFFC you can assure the timely payment to your suppliers, employees and finance providers (at all times as you want to avoid liquidity problems!)
  • it can act as a management tool and “early warning system”
  • the analysis of actuals versus forecast helps you to identify possible problems  (e.g. delay in invoicing to customers, late payments to suppliers)
  • the analysis of forecasts versus forecast helps you to identify the trend and to understand the business much better
  • the aggregated information shows if you are able to cover your financial obligations towards finance institutions/investors in the longer term and if your cash flow could meet the covenant targets or whether there will be a breach of credit facility limits. In case of a “cash rich” position it helps you to decide how much money and for which period you could invest it
  • A CFFC helps to identify foreign exchange exposures and it supports hedging decisions.

How to implement a CFFC?

Depending on the turnover, leverage, growth, systems, number of employees, internationality and currencies, the approach (and time effort) should fit the size of the organisation.

Cash flow forecasting often doesn’t have priority within organisations. However, as a treasurer, we realize the added value and need of it but also do realize that making a good CFFC could cost a lot of (time) effort. So how could we get a timely and reliable CFFC process in place without using all precious time of the finance managers?

  1. automate where possible: use either sophisticated spreadsheets, but even better, a sophisticated web based application or use the functionalities of your Treasury Management System (and fine-tune it)
  2. import centrally (via MT940) the actual banking balances where possible
  3. use your (invoice payment due dates) AP/AR data for the short term FC
  4. let fill out the “gaps” by finance managers based on their business knowledge
  5. make sure everyone reports the latest data in time with an explanation of high impact changes and actual versus realisation differences
  6. undertake actions where needed
  7. consolidate the data, analyse the information and report the highlights to the senior management on a regular basis.

 

 

 

Udo Rademakers

Treasury Consultant

Uitgelicht: Angst voor brexit jaagt bedrijven naar de beurs

| 20-05-2016 | treasuryXL |

brexit

 

Recentelijk lazen we een aantal berichten over de angst voor Brexit die meerdere bedrijven naar de beurs jaagt. (bron: FD, NRC) Onder andere Philips, Basic Fit en ASR kondigden aan naar de beurs te gaan.  treasuryXL vroeg een drietal experts om hun mening;

 

Is het inderdaad de angst voor Brexit die bedrijven naar de beurs drijft?

Douwe Dijkstra

 

Douwe Dijkstra – Owner of Albatros Beheer & Management
“Angst voor een Brexit jaagt bedrijven naar de beurs” lees ik op een aantal sites en hoorde ik in het journaal. En de beoogde investeerders dan? Die hebben dit nog niet door? Ik geloof wel in een Brexit en daardoor een eenmalige spike naar beneden van GBP en beurzen maar verwacht daarna snel herstel. Naar mijn gevoel zijn beurzen wel toe aan een rit naar boven.

 

Roger Boxman

 

Roger Boxman – Interim Risk Management Consultant
Bedrijven houden rekening met een ongunstig beursklimaat. De verwachte opbrengst zal tegenvallen bij een ‘no’ vanwege een lagere Britse Pond en een hogere vereiste risicopremie bij beleggers. Enige nuancering is op zijn plaats. Zo is Zwitserland geen lid van de EU, maar herbergt vele succesvolle multinationals. En zo heeft de Griekse toetreding tot de EU en de Euro na aanvankelijk succes de nodige rampspoed gebracht.

 

Rob Soentken

 

Rob Soëntken – ex-derivates trader
De komende maanden gaan er verscheidene Nederlandse bedrijven naar de beurs. De onzekerheden omtrent een mogelijk Brexit spelen daarbij zeker een rol. Helemaal nu het kiezer sentiment in de VS de republikeinse kandidaat Trump sterk in de kaart speelt, lijkt ook een door het volk afgedwongen Brexit een reëel mogelijke ontwikkeling. Toch moet niet vergeten worden dat deze informatie reeds in de markt is verwerkt. Dus zou men kunnen stellen dat zodra dit achter de rug is, ongeacht het resultaat, de neerwaartse druk op de beurs zou wegvallen. Niet direct, maar langzaamaan. Natuurlijk zijn er momenteel risico’s, maar die zijn ingeprijsd.