How are largest European companies managing their financial risks?
17-10-2019 | Stanley Myint | BNP Paribas
The second edition of the “Handbook of Corporate Financial Risk Management” has just been published by Risk books. The handbook is written with all risk management professionals, practitioners, instructors and students in mind, but its core readership are Treasurers at non-financial corporations. It contains 43 real life case studies covering various risk management areas. The book aims to cover both financial risk management and optimal capital structure and its contents.
Motivation for the book
This Handbook is based on real-life client discussions we had in the Risk Management Advisory team at BNP Paribas between 2005 and 2019. We noticed that corporate treasurers and chief financial officers (CFOs) often have similar questions on risk management and capital structure and that these questions are rarely addressed in the existing literature.
This situation can and should lead to a fruitful collaboration between companies and their banks. Companies often come with the best ideas, but do not have the resources to test them. Leading banks, on the other hand, have strong computational resources, a broader sector perspective, an extensive experience in internal risk management, and the ability to develop and deliver the solution. So, if they make an effort to understand a client’s problem in depth, they may be able to add considerable value.
The Handbook is the result of such an effort lasting 14 years and covering more than 700 largest European corporations from all industrial sectors. Its subject is corporate financial risk management, ie, the management of financial risks for non-financial corporations.
While there are many papers on this topic, they are generally written by academics and rarely by practitioners. If we contrast this to the subject of risk management for banks, on which many books have been written from the practitioners’ perspective, we notice a significant gap. Perhaps this is because financial risk is clearly a more central part of business among banks and asset managers than in non-financial corporations. However, that does not mean that financial risk is only important for banks and asset managers. Let us look at one example.
Consider a large European automotive company, with an operating margin of 10%. More than half of its sales are outside Europe, while its production is in EUR. This exposes the company to currency risk. Annual currency volatility is of the order of 15%, therefore, if the foreign revenues fall by 15% due to FX, this can almost wipe out the net profits. Clearly an important question for this company is, “How to manage the currency risk?”
The book blends real corporate situations across capital structure, optimal level of cash, optimal fixed-floating mix and pensions, which are particularly topical now that negative EUR yields create unpresented funding opportunities for corporates, but also tricky challenges on cost of cash and pensions management
One reason why corporate risk management has so far attracted relatively little attention in literature is that, even though the questions asked are often simple (eg, “Should I hedge the translation risk?” or “Does hedging transaction risk reduce the translation risk?”) the answers are rarely simple, and in many cases there is no generally accepted methodology on how to deal with these issues.
So where does the company treasurer go to find answers to these kinds of questions? General corporate finance books are usually very shy when it comes to discussing risk management. Two famous examples of such books devote only 20 – 30 pages to managing financial risk, out of almost 1,000 pages in total. Business schools generally do not devote much time to risk management. We hope that our book goes a long way towards filling this gap.
Website
We invite the reader to utilise the free companion website which accompanies this book, www.corporateriskmanagement.org There, you will find periodic updates on new topics not covered in The Handbook. Much like the book this website should prove a useful resource to corporate treasurers, CFOs and other practitioners as well the academic readers interested in corporate risk management.
About the authors
Stanley Myint is the Head of Risk Management Advisory at BNP Paribas and an Associate Fellow at Saïd Business School, University of Oxford. At BNP Paribas, he advises large multinational corporations on issues related to risk management and capital structure. His expertise is in quantitative and corporate finance, focusing on fixed income derivatives and optimal capital structure. Stanley has 25 years of experience in this field, including 14 years at BNP Paribas and previously at McKinsey & Company, Royal Bank of Scotland and Canadian Imperial Bank of Commerce. He has a PhD in physics from Boston University, a BSc in physics from Belgrade University and speaks French, Spanish, Serbo-Croatian and Italian. At the Saïd Business School, Stanley teaches two courses with Dimitrios Tsomocos and Manos Venardos: “Financial Crises and Risk Management” and “Fixed Income and Derivatives”.
Fabrice Famery is Head of Global Markets corporate sales at BNP Paribas. His group provides corporate clients with hedging solutions across interest rate, foreign exchange, commodity and equity asset classes. Corporate risk management has been the focus of Fabrice’s professional path for the past 30 years. He spent the first seven years of his career in the treasury department of the energy company, ELF, before joining Paribas (now BNP Paribas) in 1996, where he occupied various positions including FX derivative marketer, Head of FX Advisory Group and Head of the Fixed Income Corporate Solutions Group. Fabrice has published articles in Finance Director Europe and Risk Magazine, and has a master’s degree in international affairs from Paris Dauphine University (France).
Content:
Introduction
1 Theory and Practice of Corporate Risk Management *
2 Theory and Practice of Optimal Capital Structure *
PART I: FUNDING AND CAPITAL STRUCTURE
3 Introduction to Funding and Capital Structure
4 How to Obtain a Credit Rating
5 Refinancing Risk and Optimal Debt Maturity*
6 Optimal Cash Position *
7 Optimal Leverage *
PART II: INTEREST RATE AND INFLATION RISKS
8 Introduction to Interest Rate and Inflation Risks
9 How to Develop an Interest Rate Risk Management Policy
10 How to Improve Your Fixed-Floating Mix and Duration
11 Interest Rates: The Most Efficient Hedging Product*
12 Do You Need Inflation-linked Debt
13 Prehedging Interest Rate Risk
14 Pension Fund Asset and Liability Management
PART III: CURRENCY RISK
15 Introduction to Currency Risk
16 How to Develop an FX Risk Management Policy
17 Translation or Transaction: Netting FX Risks *
18 Early Warning Signals
19 How to Hedge High Carry Currencies*
20 Currency Risk on Covenants
21 Optimal Currency Composition of Debt 1:
Protect Book Value
22 Optimal Currency Composition of Debt 2:
Protect Leverage*
23 Cyclicality of Currencies and Use of Options to Manage Credit Utilisation *
24 Managing the Depegging Risk *
25 Currency Risk in Luxury Goods *
PART IV: CREDIT RISK
26 Introduction to Credit Risk
27 Counterparty Risk Methodology
28 Counterparty Risk Protection
29 Optimal Deposit Composition
30 Prehedging Credit Risk
31 xVA Optimisation *
PART V: M&A-RELATED RISKS
32 Introduction to M&A-related Risks
33 Risk Management for M&A
34 Deal-contingent Hedging *
PART VI: COMMODITY RISK
35 Introduction to Commodity Risk
36 Managing Commodity-linked Revenues and Currency Risk
37 Managing Commodity-linked Costs and Currency Risk
38 Commodity Input and Resulting Currency Risk *
39 Offsetting Carbon Emissions*
PART VII: EQUITY RISK
40 Introduction to Equity Risk*
41 Hedging Dilution Risk *
42 Hedging Deferred Compensation*
43 Stake-building*
Bibliography
Index
Note: Chapters marked with * are new to the second edition



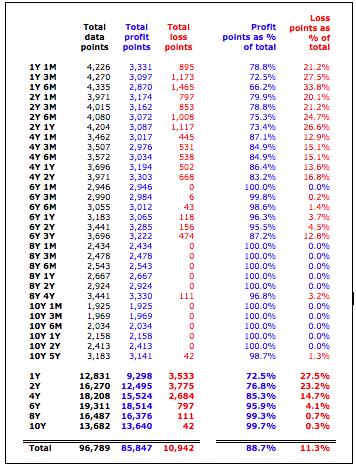
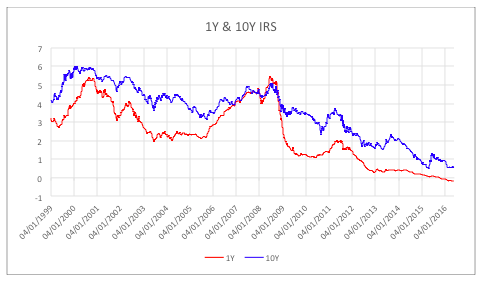
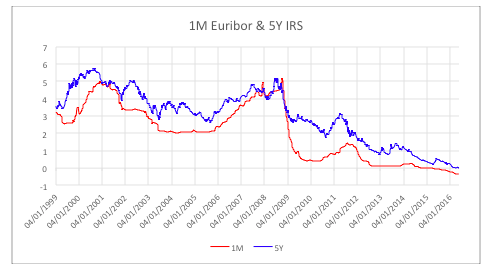
 Money Market outlook
Money Market outlook
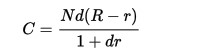 where N is the notional of the contract, R is the fixed rate, r is the published -IBOR fixing rate and d is the decimalized day count fraction over which the value start and end dates of the -IBOR rate extend.
where N is the notional of the contract, R is the fixed rate, r is the published -IBOR fixing rate and d is the decimalized day count fraction over which the value start and end dates of the -IBOR rate extend.







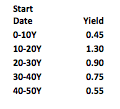
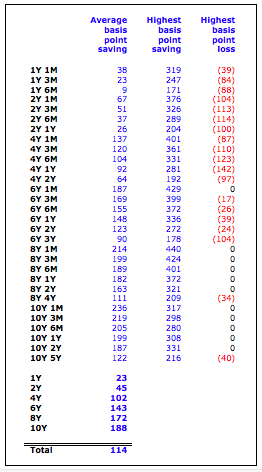
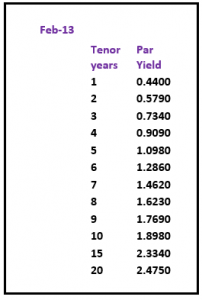
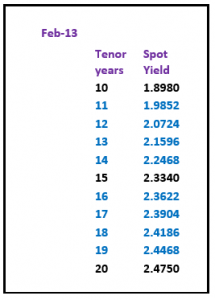
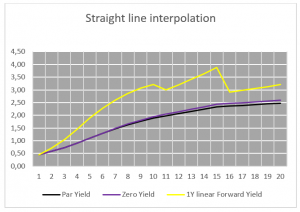
 A normal yield curve is usually upward sloping with diminishing increases in yield– the longer the tenor, the higher the interest rate. Generally it is assumed that longer maturities contain larger risks for lenders and they require adequate compensation with a risk premium in the form of a liquidity spread.
A normal yield curve is usually upward sloping with diminishing increases in yield– the longer the tenor, the higher the interest rate. Generally it is assumed that longer maturities contain larger risks for lenders and they require adequate compensation with a risk premium in the form of a liquidity spread.