Yield Curves (term structure of interest rates) – filling in the blanks
| 27-05-2016 | Lionel Pavey
Most treasurers do not have access to a dedicated financial data vendor (Bloomberg, Reuters) but are regularly faced with having to discover prices related to yield curves. There are websites that can provide us with relevant data, but these are normally a snapshot and not comprehensive – the data series is incomplete. It is therefore up to the treasurer to complete the series by filling in the blanks.
A quick refresher about the construction of a yield curve raises the following points:-
- All data must be from the same market (treasury bonds, Interest Rate Swaps (IRS) etc.)
- A regular term (maturity) is preferred for ease of construction
- A curve must be smooth
- An implied zero yield curve can be built from the smooth par curve – a theoretical yield curve where no interest is paid until maturity. In a bond this would redeem at par (100) and be issued at a deep discount to par
- A series of discounted cash flow factors (DCF) are produced
- An implied forward curve with constant maturities can be built from the par curve
- An implied forward curve must be monotonic – each point in an increasing sequence is greater than or equal to the preceding point, each point in a decreasing sequence is smaller than or equal to the preceding point
If we look at IRS par yield prices that can be found on a website, we can regularly see yield prices for periods from 1 year to 10 year inclusive, a 15 year price and a 20 year price. To construct a complete curve from 1 year up to and including 20 years we need to fill in the blanks at 11,12,13,14,16,17,18 and 19 years. These yields are assumed to be par yields – the coupon rate is equal to the yield to maturity and the instrument trades at par.
Before starting let us define the procedure for constructing a par yield curve:-
The methodology used is called “bootstrapping”. This allows us to extract discount factors (DCF) from the market rates. DCF’s allow us to calculate a value today for a cash flow in the future.
We assume that the nominal value for all calculation purposes is 100
For a 1 year rate we know the interest and redemption amount at maturity. A DCF is built whereby the net present value (NPV) of these future cash flows in 1 years’ time is equal to 100 or par.
For a 2 year rate we receive interest after 1 year and interest and redemption amount at maturity.
We discount the 1st years’ interest with the DCF we obtained from the 1 year rate and deduct this amount from our initial nominal of 100. This net amount is then divided by the interest and redemption at maturity (at end of 2 years) to obtain the DCF for the 2 year rate.
Example:
1 Year 7% 2 Year 9%
1 Year
100 / (7/100+100) = 0.93457944 (DCF)
2 Year
9 * 0.93457944 = 8.41121496
100 – 8.41121496 = 91.58878504
91.58878504 / (9/100+100) = 0.8402640829
These DCF’s can then be used to find the NPV of any cash flow maturing in 1 or 2 years’ time.
The following example shows a yield curve from February 2013 published on the website of an interbank broker.
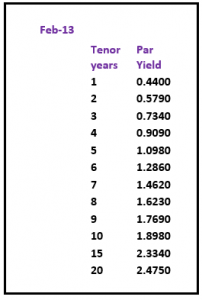
yield curve February 2013
The quickest way to price the missing periods would be with straight line interpolation of the par curve between the known points – which would produce the following par curve, zero yield curve and forward curve with constant 1 year maturity.
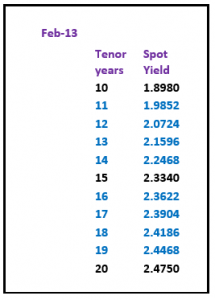
yield curve February 2013
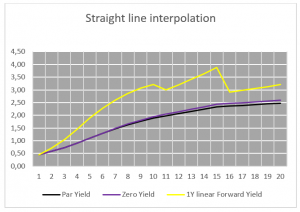
Straight line interpolation
Whilst the par curve and zero curve are smooth, the implied 1 year constant maturity curve is jagged and certainly neither smooth nor monotonic. The 11th 1 year period rate is lower than the 10th period and the 15th 1 year period rate is higher than the 16th period.
A second approach would be to apply a weighting to the known periods of the par curve and to average the difference out over the missing periods. Read more on this second approach in my next article which will appear next week.

Treasurer









