Option Tales: Cheap Options Part III
| 31-05-2016 | Rob Söentken
Today in Rob Söentken’s Option Tales: When buying options it is tempting to see if the premium expenses can be minimized. A number of solutions are possible, which will be discussed in four articles. In the previous article I talked about choosing the longer tenor and the compound option. Today I will discuss the average rate option (ARO) and the conditional premium option.
Average Rate Option (ARO)
An Average Rate Option (ARO) can be misleading because it is like a vanilla option except for the reference rate against which it is exercised. The reference rate for an ARO is an average based on spot rates for USD taken at predetermined intervals. For a vanilla option it is the single rate for spot at maturity. If the intention was to hedge the rate for USD in 1-year time, the average of USD rates during the year is really something different.
If we would be looking to hedge a 1-year tenor and the averaging would be at quarterly intervals, a rough and quick estimate of an ARO’s cost would be the average premium of separate vanilla options for respective tenors, in this case that would be 0.9% (see diagram 3). Which would be considerably less than a vanilla option costing 1.50%.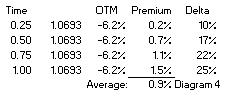
But unlike a strip of options which can be exercised individually, an ARO can only be exercised in total. At maturity the averaging of the fixings is mostly done, and it could happen that while the last fixing is In The Money (ITM), the average of the fixings is not, making the ARO expire worthless. In this example it would be advantageous to have a strip of vanilla options because each option would be exercisable independently of the other. The ARO on the other hand is worthless because the average would still be above the strike. This inherent risk in using an ARO will make the premium of an ARO even a bit cheaper than a strip of vanilla options.
The bottom line remains that the premium of an ARO is lower than a vanilla option for the same tenor, because the embedded tenor of the ARO is really shorter. The effect is comparable to paragraph 2 ‘Choose shorter tenor’. Slightly worse even when considering the averaging effect.
Conditional Premium Option
A Conditional Premium Option has the advantage over a vanilla option in that premium only has to be paid if the option is In-The-Money (ITM). But… if the option is ITM the premium will be a multiple of a vanilla option. The premium of such a Conditional Premium Option is calculated by dividing the premium of a vanilla option
(1.5%, see diagram 5) by the chance it will be exercised (Delta, in this case 25%), ie 1.5% : 25% = 6%. It could be a very disappointing to find that if this Conditional Premium option is only marginally ITM at maturity, because the premium of 6% still has to be paid.
A Conditional Premium Option is constructed by buying a vanilla option and selling a digital option with the same strike. The digital option will be for a payout of 6% and because it also has a chance on exercise of 25% it will generate 1.5% premium, offsetting the premium of the vanilla option.
Next week in the last Option Tales article; the Reverse Knock-Out Option (RKO).
Would you like to read more on Rob Söentken’s Option Tales?:
2. ATM or OTM
3. Cheap Options part I
Ex-derivates trader
