Managing treasury risk: Interest rate risk (Part II)
|31-1-2017 | Lionel Pavey |

There are lots of discussions concerning risk, but let us start by trying to define what we mean by risk. In my first article of this series I wrote about risk managment and what the core criteria are for a solid risk management policy. Today I want to focus on interest rate risk. There are 4 types of interest rate risk.
Absolute Interest Rate Risk
Absolute interest rate risk occurs when we are exposed to directional changes in rates – either up or down. This is the main area of rate risk that gets monitored and analysed within a company as it is immediately visible and has a potential effect on profit.
Yield Curve Risk
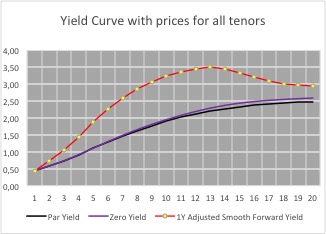
Yield curve risk occurs from changes between short term rates and long term rates, together with changes in the spreads between the underlying periods. Under normal circumstances a yield curve would be upward sloping if viewed as a graph. The implication is that longer term rates are higher than short term rates because of the higher risk to the lender and less liquidity in the market for long dated transactions. Changes to the yield curve (steepening or flattening) can have an impact on decisions for investment and borrowings, leading to changes in profit.
Refunding or Reinvestment Risk
Refunding or reinvestment risk occurs when borrowings or investments mature at a time when interest rates are not favourable. Borrowings or investments are rolled over at rates that had not been forecast leading to a potential loss on projects or investments.
Embedded Options Risk
Embedded options are provisions in securities that cannot be traded separately from the security and grant rights to either the issuer or the holder that can introduce additional risk. Benefits for the issuer can include a call option, a right to repay before maturity without incurring a penalty, an interest rate cap. Benefits for the holder can include a put option, a conversion right via convertible bonds, an interest rate floor.
An attempt can be made to calculate the interest rate risk on either a complete portfolio or on individual borrowings or investment. This is done by comparing the stated interest rate to the actual or projected interest rate. Methods include:
- Mark to market
- Parallel shift in the whole yield curve
- Tailor-made shift in the whole yield curve
- Duration, DV01, Convexity
- Value at Risk (VaR)
These are all forms of quantitative analysis and well recognized. Personally I am of the opinion that VaR is not a very good method for interest rates. Interest rates do not display normal Gaussian distribution – they do not resemble a normal bell curve. Interest rate distribution curves display fat tails compared to normal statistical models.
Financial products that are commonly used to manage interest rate risk include FRAs, Futures, Caps, Floors, Collars, Options, Interest Rate Swaps and Swaptions.

Cash Management and Treasury Specialist
More articles from this author:
The impact of negative interest rates
How long can interest rates stay so low?

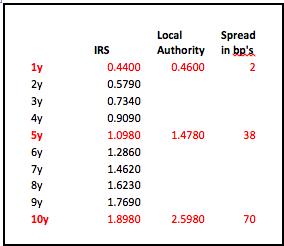
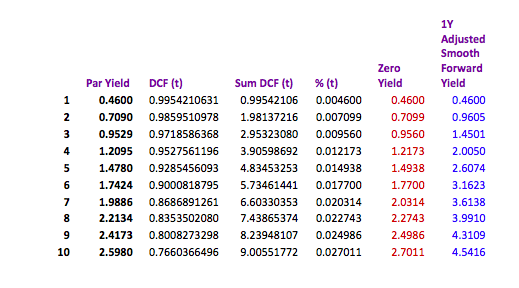
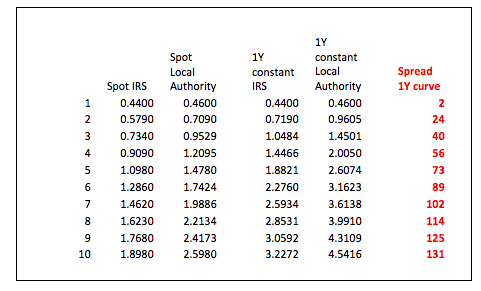
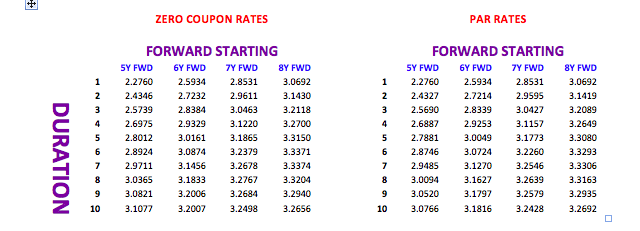
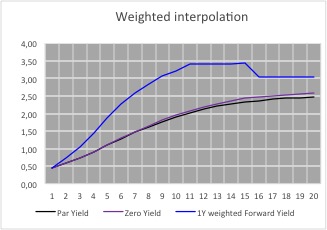
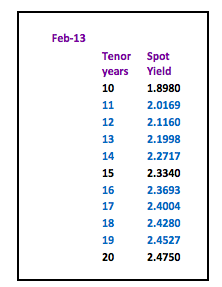
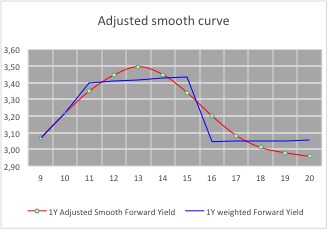
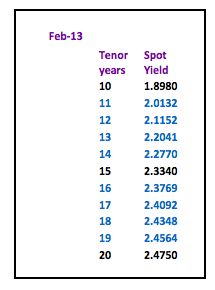
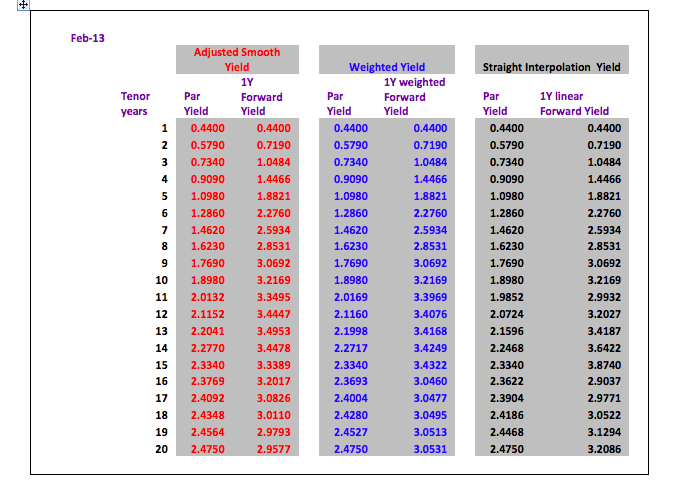
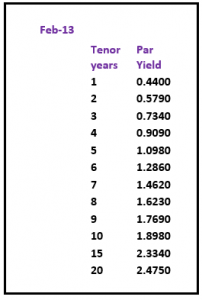
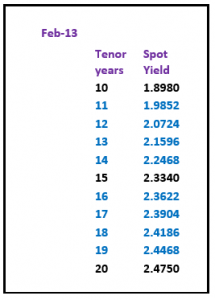
 So far in this series we have constructed yield curves based on Interest Rate Swaps. This route was chosen as Swaps provide the benchmark for pricing many loan products. Let us look at constructing a yield curve for local authority loans. Yet again, the choice has been made for a product where prices are published on a daily basis.
So far in this series we have constructed yield curves based on Interest Rate Swaps. This route was chosen as Swaps provide the benchmark for pricing many loan products. Let us look at constructing a yield curve for local authority loans. Yet again, the choice has been made for a product where prices are published on a daily basis.